接觸角量測原理
OCA 系列的光學接觸角測量和輪廓分析系統將高分辨率光學、精確的液體劑量和精確的樣品定位結合到強大且可靠的測量系統中。 本文將著介紹 OCA 系列中靜滴法、懸滴法及固體表面能測定原理的說明。
點擊快速找到原理:
接觸角的形成
接觸角是指在液體/氣體界面接觸固體表面而形成的夾角,許多界面現像出現在三相相遇的情況下,最常見的情況是固體、液體和氣體之間的接觸。因為界面張力和表面張力的切向力平衡,使系統處於穩定狀態,讓固體、液體和氣體之間的接觸線靜止
表面能與界面張力的作用力
當液體與固體和氣體接觸時,會在三相接觸線處形成一個平衡接觸角 θC。這個角度反映了液體在固體表面的潤濕性。
.png)
固體的表面能(σS):沿固體表面作用
固-液界面能(σSL):朝相反方向作用
液體的表面張力(σL):沿液滴表面的切線方向作用
在液體和固體之間的接觸平面上的矢量投影產生了 Young 方程:
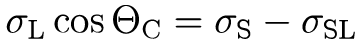
由於固體的表面能和固-液界面能通常是未知的,因此需要使用特定模型來考慮液體和固體之間的不同相互作用,以確定這些參數。
接觸角的極值與應用
| 接觸角極值 | 現象 | 應用 |
|---|---|---|
| 完全潤濕 (接觸角 0°) |
液滴完全擴散,形成一層薄膜(單分子厚度) | 小接觸角材料: 染料和清漆行業,需要液體均勻分佈以獲得最佳效果。 |
| 完全去濕 (接觸角 180°) |
液滴形成球形,僅在一個點上接觸固體 | 大接觸角材料: 蓮花效應的陶瓷,水滴滾落表面,不留污漬,適合用於防水、防污塗層 |
固定液滴法
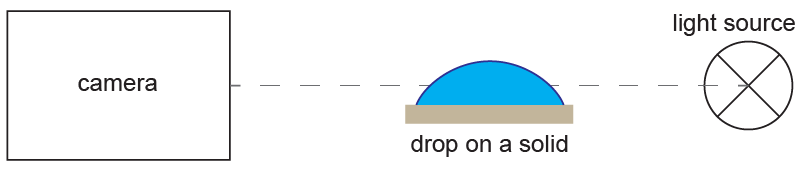
▲固著滴法的示意圖設置
DataPhysics 軟體評估接觸角的五種輪廓分析系統
- 切線方法:透過對記錄圖像的灰度值進行分析,可以清楚辨識出所謂的基線(液滴與固體之間的接觸點)以及液滴的輪廓
.png)
- 高度/寬度方法:將液滴的輪廓擬合為一個圓形,透過純數學計算來描述液滴的形狀。方法相對簡單,適合形狀接近圓形的小液滴
- 橢圓方法:使用橢圓形曲線來擬合液滴的輪廓,適合處理較為拉長的液滴形狀。此方法同樣基於數學擬合,但比高度/寬度方法更加靈活。
- 多項式方法:採用高階多項式來描述液滴的輪廓,能夠處理形狀較複雜的液滴。雖然是一種純數學模型方法,但提供更高的擬合自由度
- Young-Laplace 方法:基於液滴的物理特性進行計算,考慮了局部重力加速度、液體密度與周圍介質密度等參數。適合大接觸角和大液滴,通常能產生最可靠的結果。然而,由於假設液滴的下降輪廓是對稱的,因此只提供基線左右交點的共同接觸角。
懸滴法—光學接觸角測量
使用高解析度影像技術,快速捕捉掛在給藥針上的液滴圖像,然後使用軟體對其進行分析
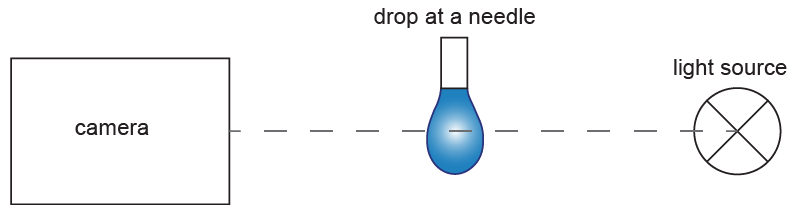
▲懸滴法的示意圖設置
影響液滴形狀的主要因素
一、表面張力
傾向於最小化液滴的表面積,使液滴形成接近球形的形狀,反映了液體分子之間的吸引力,促使液滴穩定,尤其是小夜滴中表面張力起主導作用
Young-Laplace 方程
液滴的形狀可以透過 Young-Laplace 方程進行分析。該方程描述了彎曲液體表面或界面內外部壓力差(稱為拉普拉斯壓力)與液滴主曲率半徑 Ri的關係,當表面張力主導時,壓力差(ΔPDelta PΔP)促使液滴更接近球形。
.png)
二、重力
液滴在重力作用下,會被拉長並偏離球形,最終形成典型的梨狀形狀,重力的影響越大,液滴的形狀越接近非對稱的懸垂形態,當液滴足夠大時,重力的影響變得顯著,壓力分佈也隨高度發生明顯變化。
帕斯卡定律(靜水壓力原理)
重力會在 z 軸上產生壓力差,因此液滴內部壓力的分佈如何隨高度而改變,重力越大,壓力分佈的不均勻性越明顯,液滴形狀越偏離對稱球形
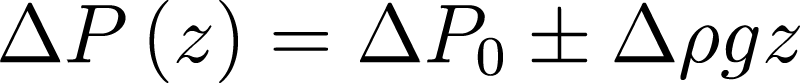
對於懸滴上的 Young-Laplace 擬合的推導
.png)
理論液滴形狀與相機記錄的液滴形狀進行數值擬合後,可最終計算出液體的表面張力。如果液滴周圍的介質不是空氣而是另一種液體,這些方法同樣適用,此時可進一步評估液體間的界面張力。此外,Young-Laplace 擬合還可用於分析液滴在固體表面上的形狀變化,從而確定固著液滴法中液滴的接觸角。
對於懸垂水滴,頂點(水滴的最低點)的主曲率半徑為:R1=R2=R。因此,將參考平面放置在該點很方便。對於上面的每個點,它都滿足 R2=x/sin Φ(見圖 2)。上述等式導致:
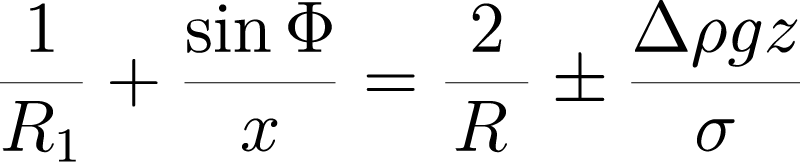
▲插入半徑在距離 z 處的拉普拉斯壓力
使用水滴形狀的弧長 s 引入參數化導致以下三個具有三個邊界值的一階微分方程組,可以通過數值程序求解:
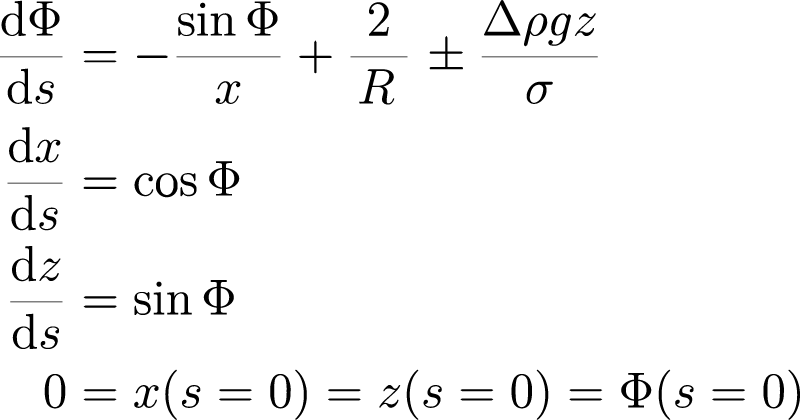
▲懸垂法微分方程
固體表面能
透過測量液滴在固體表面上的接觸角,再結合已知的液體表面張力數據(包括色散和極性部分),使用模型計算固體與液體間的界面張力,進而推算出固體的表面能。
OWRK 模型
是一個常用來計算固體表面能的數學模型,利用液體和固體的色散力和極性力的幾何平均值來計算它們的界面張力,以確定固體的表面能。
將OWRK 方程代入(圖一) Young 方程中,可以得到 y=mx+c 的線性方程(圖二),用於確定表面能的回歸線(圖三)
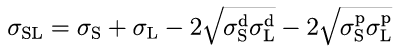
▲ 圖一:OWRK 方程
▲ 圖二: y=mx+c 的線性方程
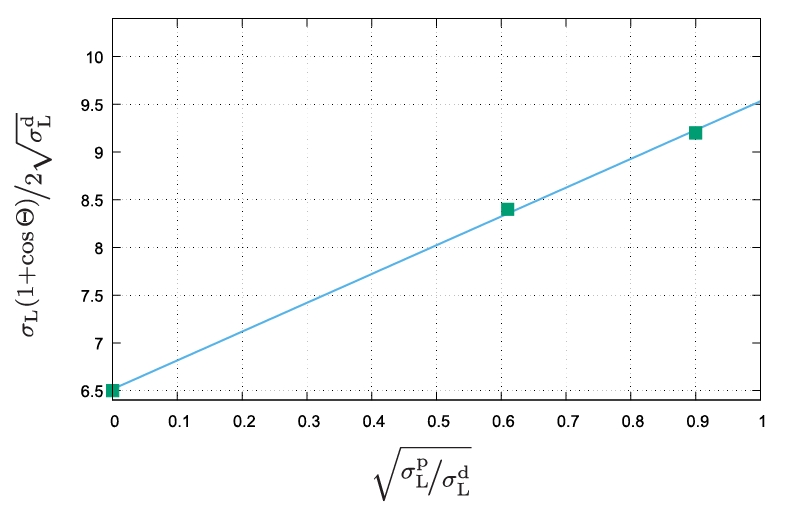
▲ 圖三:確定表面能的回歸線
在這個方程中,c代表固體表面能的色散部分;m 代表固體表面能的極性部分,x 則是由液體表面張力的極性和色散部分計算得出;y 由接觸角和液體表面張力計算得出,因此當測量至少兩種測試液體的接觸角時,可以評估這些參數以創建回歸線。
由於僅依據兩個測試點建立的回歸線無法充分反映結果的準確性,因此建議至少使用三種測試液體進行接觸角測量。常見的測試液體包括二碘甲烷、乙二醇和硫二甘醇,這些液體通常能提供良好的測試結果。此外,OCA 軟件能自動完成上述測試與評估,並且除了支持 OWRK 模型外,還提供另外八種理論模型,用於計算固體的表面能。
德國 dataphysics 作為全球表面測量儀器的知名廠家,專業致力於為全球表面化學實驗室提供解決方案,產品覆蓋多個國家,擁有高水平的研發隊伍,為不斷擴展儀器功能和提升儀器質量而不斷努力
延伸閱讀
右滑更多看更多文章>>
.jpg)
.jpg)
.jpg)


.png)

.png)