因為粒子的表面由於電子的存在而產生電磁場,並且由於光代表電磁輻射,所以它可以相互作用產生一種被描述為米氏散射或衍射的現象。 Mie 散射以及相應的 Mie 理論以德國物理學家 Gustav Mie (1868-1957) 的名字命名,他在 20 世紀初首次計算了這種現象。
米氏散射,在入射光方向上離粒子一定距離,是一種模式,將根據粒子的大小和入射光的波長而發展。從這個 Mie 散射圖案中可以獲得與材料尺寸分佈相關的信息。
有些材料不透光並吸收能量。在這些情況下,可以假設該物質具有極高的折射率以及很大的虛構成分(參見下面的透明粒子)。在這些條件下,計算可以是弗勞恩霍夫理論所描述的那些。
光也可以從物質表面反射,使用這些數據進行尺寸測量將是一個不同的問題。
第三次發生的相互作用是當材料有點透明時發生的一種特殊情況。在這種情況下,光穿過粒子就像穿過鑽石一樣。在鑽石的情況下,它會折射並產生眾所周知的閃光;然而,當穿過一個粒子時,它可能會增加米氏散射/衍射圖案。這種影響將在下面討論。
米氏散射與哪些條件相關:
如上所述,衍射/米氏散射僅取決於粒子的大小。反射對衍射沒有影響,但如果表面足夠反射,則可能會影響折射。對折射的影響將是限制進入粒子的光量,從而減少折射對衍射圖案的影響。
折射可以對衍射/米氏散射模式產生相當大的影響,但影響的大小很大程度上取決於材料的尺寸和形狀。
球體將傳輸相同的折射圖案,無論其方向如何。在球形顆粒相對於入射光不斷改變方向的測量系統中,圖案總是相同的,並且會產生明確的、強化的無關信息,這些信息可能會扭曲或乾擾通過衍射計算顆粒大小圖案。 (圖1)
如上所述,衍射/米氏散射僅取決於粒子的大小。反射對衍射沒有影響,但如果表面足夠反射,則可能會影響折射。對折射的影響將是限制進入粒子的光量,從而減少折射對衍射圖案的影響。
折射可以對衍射/米氏散射模式產生相當大的影響,但影響的大小很大程度上取決於材料的尺寸和形狀。
球體將傳輸相同的折射圖案,無論其方向如何。在球形顆粒相對於入射光不斷改變方向的測量系統中,圖案總是相同的,並且會產生明確的、強化的無關信息,這些信息可能會扭曲或乾擾通過衍射計算顆粒大小圖案。 (圖1)
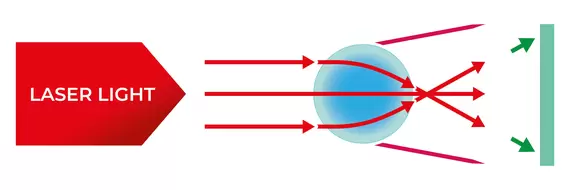
圖一、散射光集中在一處,翻滾沒有效果。
折射的影響也受到粒子形狀的強烈影響。非球形的也可以折射光並且可以產生與球形顆粒一樣疊加在衍射圖案上的散射圖案。但是,效果有些不同。
請記住,粒子處於運動狀態,並且會因運動而翻滾。每次方向的變化都會為光線進入和折射提供一個新的和不同的表面。在退出時,會出現一個新的折射圖案,該圖案疊加在衍射圖案上。
沒有出現用球形顆粒觀察到的增強效果。折射圖案作為某種恆定圖案在衍射圖案上散佈,並且對衍射圖案的影響程度遠小於球形顆粒。 (圖2)
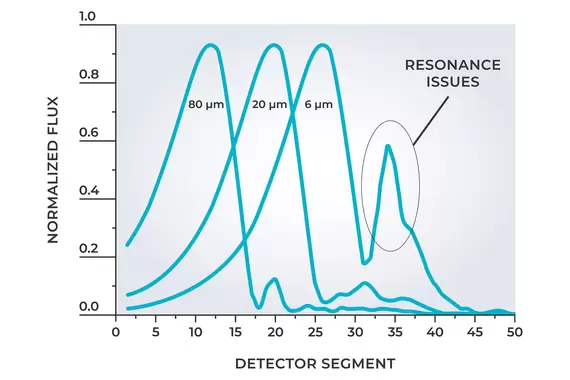
次峰是由通過球體折射並從表面衍射出的光產生的圖案的干涉(組合)
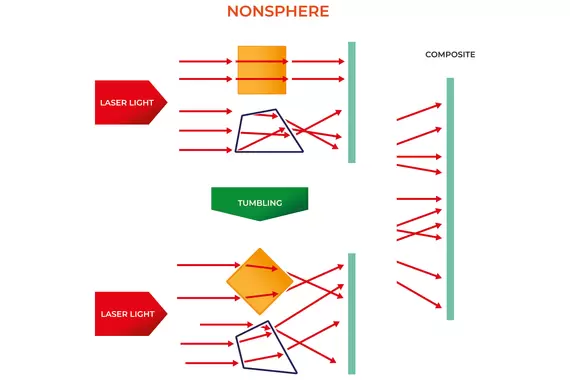
圖2:散射光散佈在各處,並不集中在任何一個地方。 因此,不規則形狀的顆粒對折射率的影響遠小於球形顆粒,校正也少得多。
如何糾正折射可能導致的衍射圖案中的潛在誤差:
所需的 Mie 理論:對於球形粒子,可以使用 Gustav Mie 開發的理論中體現的廣為接受的概念。這種補償通常被稱為“米氏理論”,它描述了球形對光的影響。米氏理論包括粒子的折射率與周圍介質的折射率以及透明材料的散射效率相關的方面。散射效率可以理解為材料散射光的相對能力。根據 Mie 理論,散射量將隨尺寸非線性變化。
不需要 Mie 理論:如果材料不透明(例如炭黑),則不需要 Mie 理論對折射進行補償,但必須包括散射效率的計算。對於 Microtrac 儀器,深色顏料、炭黑和金屬等材料被認為具有吸光性(不透明)。 Microtrac 軟件中的適當選擇解決了可以使用弗勞恩霍夫理論計算的這種情況。
不需要 Mie 理論:如果材料不透明(例如炭黑),則不需要 Mie 理論對折射進行補償,但必須包括散射效率的計算。對於 Microtrac 儀器,深色顏料、炭黑和金屬等材料被認為具有吸光性(不透明)。 Microtrac 軟件中的適當選擇解決了可以使用弗勞恩霍夫理論計算的這種情況。
透明粒子的光散射:
只考慮透明粒子的情況。還要考慮折射率有兩個項,它們可能被認為在某種程度上彼此獨立。這兩個由折射率的實分量和虛分量的名稱來識別。根據“米氏理論”,每一種對補償和散射效率都有特定的影響。折射率對光散射沒有影響的假設(在炭黑的情況下是正確的)將把米氏理論簡化為著名的弗勞恩霍夫衍射理論。如果在粒子是透明的情況下應用夫瑯禾費衍射,則在確定尺寸分佈時可能會出現錯誤,因此需要對球形粒子進行 Mie 理論或對非球形粒子進行其他補償。
N= m-ik 其中 N 是總折射率,它是物質與真空相比的實部 (m) 和虛部 (ik) 的組合。該術語源自對複數的研究。在使用懸浮在流體中的顆粒進行尺寸測量的情況下,k 值代表消光係數(與材料的吸收係數和波長有關),i 是 √-1,m 是相對折射率(RI樣品/ RI 流體中的每一個都已與真空進行比較)。總而言之,純衍射光是用於尺寸測量的理想信息。相對折射率定義了出射光將聚焦和擴散的位置,而虛部表示折射光的強度。如果虛部非常低,則折射強度會很高。
因此,對於氧化鋁,方程為 N= 1.76/1.33 - ik。該等式可以通過知道 ik 的值來實現。不幸的是,這些值在文獻中並不容易獲得,並且難以通過實驗獲得。使用虛部的另一個考慮因素是評估其在計算 N 和 Mie 補償中的影響。
由於此討論是一種非數學的、解釋性的、概念性的方法,因此未提供以下數學證明,但鼓勵讀者研究該領域,因為它是從 Maxwell 的處理中充分發展起來的。 RI 值及其對粒子的相應虛部的影響總結如下。
總結:
除了 1-10 微米區域外,總折射率的虛部對通過粒子的光的折射幾乎沒有影響。 即使在這個尺寸範圍內,當虛構成分是炭黑 (0.66i) 或更高級別(反射金屬)時,效果也很重要。
在非球形顆粒的情況下,折射率通常對計算的尺寸分佈影響較小,但仍需要從半經驗確定的數據中進行少量補償。 在這種情況下,虛部沒有意義,可以忽略不計。 一般來說,虛分量可以被描述為對衍射光散射粒子測量的影響可以忽略不計,除非在非常特殊的情況下,這種情況很少遇到。
N= m-ik 其中 N 是總折射率,它是物質與真空相比的實部 (m) 和虛部 (ik) 的組合。該術語源自對複數的研究。在使用懸浮在流體中的顆粒進行尺寸測量的情況下,k 值代表消光係數(與材料的吸收係數和波長有關),i 是 √-1,m 是相對折射率(RI樣品/ RI 流體中的每一個都已與真空進行比較)。總而言之,純衍射光是用於尺寸測量的理想信息。相對折射率定義了出射光將聚焦和擴散的位置,而虛部表示折射光的強度。如果虛部非常低,則折射強度會很高。
因此,對於氧化鋁,方程為 N= 1.76/1.33 - ik。該等式可以通過知道 ik 的值來實現。不幸的是,這些值在文獻中並不容易獲得,並且難以通過實驗獲得。使用虛部的另一個考慮因素是評估其在計算 N 和 Mie 補償中的影響。
由於此討論是一種非數學的、解釋性的、概念性的方法,因此未提供以下數學證明,但鼓勵讀者研究該領域,因為它是從 Maxwell 的處理中充分發展起來的。 RI 值及其對粒子的相應虛部的影響總結如下。
總結:
除了 1-10 微米區域外,總折射率的虛部對通過粒子的光的折射幾乎沒有影響。 即使在這個尺寸範圍內,當虛構成分是炭黑 (0.66i) 或更高級別(反射金屬)時,效果也很重要。
在非球形顆粒的情況下,折射率通常對計算的尺寸分佈影響較小,但仍需要從半經驗確定的數據中進行少量補償。 在這種情況下,虛部沒有意義,可以忽略不計。 一般來說,虛分量可以被描述為對衍射光散射粒子測量的影響可以忽略不計,除非在非常特殊的情況下,這種情況很少遇到。
